INECUACIONES
Qué es una inecuacion?
En matemática, una inecuación es una desigualdad algebraica en la que aparecen una o más incógnitas en los miembros de la desigualdad. Si la desigualdad es del tipo  o
o 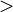 se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥ se denomina inecuación en sentido amplio.
se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥ se denomina inecuación en sentido amplio.
Del mismo modo en que se hace la diferencia de igualdad y ecuación, una inecuación que es válida para todas las variables se llama inecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.Los valores que verifican la desigualdad, son sus soluciones. o
o 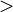 se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥ se denomina inecuación en sentido amplio.
se denomina inecuación en sentido estricto y si es del tipo ≤ o ≥ se denomina inecuación en sentido amplio.
- Ejemplo de inecuación incondicional:
 .
. - Ejemplo de inecuación condicional:
 .
.
Clasificación
Los criterios más comunes de clasificación del ejemplo: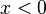 .
.-
- De dos incógnitas. Ejemplo:
 .
. - De tres incógnitas. Ejemplo:
 .
. - etc.
- De dos incógnitas. Ejemplo:
- Según la potencia de la incógnita,
- De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo:
 .
. - De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo:
 .
. - De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo:
 .
. - etc.
- De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo:
Inecuaciones de segundo grado con una incógnita
Se expresan a través de cualquiera de las desigualdades siguientes (con a, b y c números reales, y a distinto de cero):Sistema de inecuaciones
Véase también: Programación lineal
La región de viabilidad en un problema de programación lineal está definida por un sistema de inecuaciones.
Sistema de inecuaciones de primer grado con una incógnita
Es un conjunto de inecuaciones de primer grado con la misma variable:La solución del sistema será el conjunto de números reales que verifican a la vez todas las inecuaciones.
Las inecuaciones son desigualdades algebraicas en la que sus dos miembros se relacionan por uno de estos signos:
| < | menor que | 2x − 1 < 7 |
| ≤ | menor o igual que | 2x − 1 ≤ 7 |
| > | mayor que | 2x − 1 > 7 |
| ≥ | mayor o igual que | 2x − 1 ≥ 7 |
La solución de una inecuación es el conjunto de valores de la variable que la verifica.
La solución de la inecuación se expresa mediante:
1. Una representación gráfica.
2. Un intervalo.
2x − 1 < 7
2x < 8 x < 4

(-∞, 4)
2x − 1 ≤ 7
2x ≤ 8 x ≤ 4

(-∞, 4]
2x − 1 > 7
2x > 8 x > 4

(4, ∞)
2x − 1 ≥ 7
2x ≥ 8 x ≥ 4

[4, ∞)
Inecuaciones equivalentes
Si a los dos miembros de una inecuación se les suma o se les resta un mismo número, la inecuación resultante es equivalente a la dada.
3x + 4 < 5 3x + 4 − 4 < 5 − 4 3x < 1
Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número positivo, la inecuación resultante es equivalente a la dada.
2x < 6 2x : 2 < 6 : 2 x < 3
Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número negativo, la inecuación resultante cambia de sentido y es equivalente a la dada.
−x < 5 (−x) · (−1) > 5 · (−1) x > −5
Inecuaciones de primer grado
Inecuaciones de primer grado con una incógnita
1º Quitar corchetes y paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x a un lado de la desigualdad y los términos independientes en el otro.
4º Efectuar las operaciones
5º Si el coeficiente de la x es negativo multiplicamos por −1, por lo que cambiará el sentido de la desigualdad.
6º Despejamos la incógnita.
7º Expresar la solución de forma gráfica y con un intervalo.
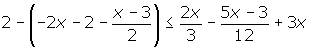
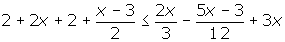
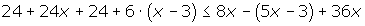
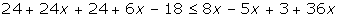
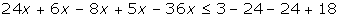
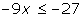
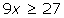
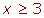
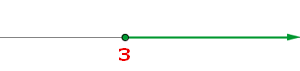
[3, +∞)
Inecuaciones de segundo grado
Consideremos la inecuación:
x2 − 6x + 8 > 0
La resolveremos aplicando los siguientes pasos:
1ºIgualamos el polinomio del primer miembro a cero y obtenemos las raíces de la ecuación de segundo grado.
x2 − 6x + 8 = 0
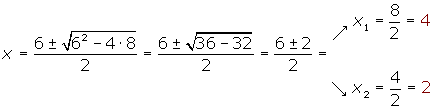
2º Representamos estos valores en la recta real. Tomamos un punto de cada intervalo y evaluamos el signo en cada intervalo:

P(0) = 02 − 6 · 0 + 8 > 0
P(3) = 32 − 6 · 3 + 8 = 17 − 18 < 0
P(5) = 52 − 6 · 5 + 8 = 33 − 30 > 0
3º La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que el polinomio.

S = (-∞, 2)  (4, ∞)
(4, ∞)
 (4, ∞)
(4, ∞)
x2 + 2x +1 ≥ 0
x2 + 2x +1 = 0
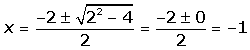
(x + 1)2 ≥ 0
Como un número elevado al cuadrado es siempre positivo la solución es 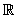
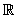
| Solución | ||
|---|---|---|
| x2 + 2x +1 ≥ 0 | (x + 1)2 ≥ 0 | 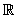 |
| x2 + 2x +1 > 0 | (x + 1)2 > 0 | |
| x2 + 2x +1 ≤ 0 | (x + 1)2 ≤ 0 | x = − 1 |
| x2 + 2x +1 < 0 | (x + 1)2 < 0 | 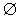 |
x2 + x +1 > 0
x2 + x +1 = 0
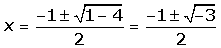
Cuando no tiene raíces reales, le damos al polinomio cualquier valor si:
El signo obtenido coincide con el de la desigualdad, la solución es 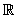 .
.
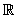 .
.
El signo obtenido no coincide con el de la desigualdad, no tiene solución.
| Solución | |
|---|---|
| x2 + x +1 ≥ 0 | 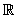 |
| x2 + x +1 > 0 | 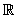 |
| x2 + x +1 ≤ 0 | 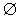 |
| x2 + x +1 < 0 | 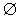 |
Inecuaciones racionales
Las inecuaciones racionales se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero.
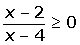
1º Hallamos las raíces del numerador y del denominador.
x − 2 = 0 x = 2
x − 4 = 0 x = 4
2º
Representamos estos valores en la recta real, teniendo en cuenta que
las raíces del denominador, independientemente del signo de la
desigualdad, tienen que ser abiertas.
3ºTomamos un punto de cada intervalo y evaluamos el signo en cada intervalo:

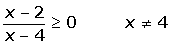




4º La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que la fracción polinómica.
S = (-∞, 2]  (4, ∞)
(4, ∞)
 (4, ∞)
(4, ∞) 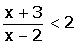
Pasamos el 2 al primer miembro y ponemos a común denominador.
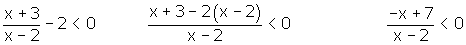
Hallamos las raíces del numerador y del denominador.
−x + 7 = 0 x = 7
x − 2 = 0 x = 2
Evaluamos el signo:


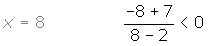

S = (-∞, 2)  (7, ∞)
(7, ∞)
 (7, ∞)
(7, ∞) 
Para resolver desigualdades de segundo grado o de grado superior es necesario descomponer en factores. Recuerda que para hacer la descomposición factorial dependiendo de la ecuación podemos sacar factor común, resolver la ecuación de segundo grado o aplicar la regla de Ruffini.


Inecuaciones con denominadores


Inecuaciones de grado superior a dos



Inecuaciones fraccionarias
| ||||||
Inecuaciones fraccionarias. Inecuaciones en las que cada término es una fracción racional, o cociente de polinomios.
Definición
Inecuaciones: Desigualdades algebraicas en la que sus dos miembros se relacionan por los signos: mayor, menor, mayor o igual o menor o igual. La solución de una inecuación es el conjunto de valores de la variable que la verifica, donde la solución se expresa mediante una representación gráfica y/o mediante un intervalo.Para dar solución a una inecuación hay que tener en cuenta que:
- Una inecuación se verifica solo para algunos valores de las variables.
- Los valores numéricos para los cuales se verifica la desigualdad son las soluciones de la misma.
- Resolver una inecuación consiste en hallar los valores numéricos para los cuales la desigualdad es verdadera.
Regla general para resolver una inecuación
Se sigue el mismo procedimiento que para resolver una ecuación (quitar denominadores, términos, agrupar, etc), pero hay que tener en cuenta, al multiplicar o dividir por cantidades negativas que se debe de cambiar el sentido de la desigualdad para que el resultado no varíe.Método de resolución de las inecuaciones fraccionarias
Las inecuaciones fraccionarias o racionales tienen incognitas tanto en el numerador como en el denominador y se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero.Para encontrar la solución hay que descomponer factorialmente los polinomios numerador y denominador, aplicando Ruffini, complitud de cuadrados, etc. … el método que consideres más apropiado o que mejor te resulte. Una vez descompuestos nunca simplificar ya que se podrían perder soluciones. Posteriormente se procede como con las inecuaciones de grado mayor que uno, ya que se trata en el fondo de averiguar el signo final que va a tener un cociente de productos de binomios.
Ejemplos de inecuaciones fraccionarias
Ejemplo 1- Se calculan las raíces del numerador y del denominador.
x=2
x-4=0
x=4
- Se representan estos valores en la recta real, teniendo en cuenta que las raíces del denominador, independientemente del signo de la desigualdad, tienen que ser abiertas.
- Se toma un punto de cada intervalo y se evalúa el signo en cada intervalo.
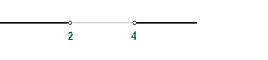

- La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que la fracción polinómica.
Otro ejemplo:

S = (-∞, 2)υ (7, ∞)
Algunos videos que púeden aclarar tus dudas:
Fuentes bibliograficas:
http://es.wikipedia.org/wiki/Inecuaci%C3%B3nhttp://es.wikipedia.org/wiki/Inecuaci%C3%B3n
http://www.vitutor.com/ecuaciones/ine/ine0_Contenidos.html
http://www.vitutor.com/ecuaciones/ine/ine1_Contenidos.html
http://www.ditutor.com/inecuaciones/inecuaciones.html
http://www.vadenumeros.es/cuarto/resolver-inecuaciones.htm
gracias¡¡¡¡¡¡¡¡¡¡¡






